How Do You Know if Something Is a a Catalyst

2.10: Zero-Guild Reactions

1. Final updated

2. Save as PDF

Page ID

1451

In some reactions, the rate is patently contained of the reactant concentration. The rates of these nil-order reactions practise not vary with increasing nor decreasing reactants concentrations. This means that the rate of the reaction is equal to the charge per unit abiding, \(thousand\), of that reaction. This property differs from both first-social club reactions and second-order reactions.

Origin of Zero Order Kinetics

Zero-guild kinetics is ever an artifact of the conditions nether which the reaction is carried out. For this reason, reactions that follow zero-order kinetics are often referred to every bit pseudo-null-order reactions. Clearly, a zero-order process cannot continue later a reactant has been wearied. Just before this signal is reached, the reaction will revert to another rate police instead of falling straight to cypher equally depicted at the upper left.

There are two general conditions that tin give rise to cypher-order rates:

1. Merely a small fraction of the reactant molecules are in a location or country in which they are able to react, and this fraction is continually replenished from the larger pool.
2. When two or more reactants are involved, the concentrations of some are much greater than those of others

This state of affairs commonly occurs when a reaction is catalyzed by attachment to a solid surface (heterogeneous catalysis) or to an enzyme.

Example 1: Decomposition of Nitrous Oxide

Nitrous oxide volition decompose exothermically into nitrogen and oxygen, at a temperature of approximately 575 °C

\[\ce{2N_2O ->[\Delta, \,Ni] 2N_2(g) + O_2(g)}\]

This reaction in the presence of a hot platinum wire (which acts every bit a goad) is zero-guild, but it follows more conventional second gild kinetics when carried out entirely in the gas phase.

\[\ce{2N_2O -> 2N_2(g) + O_2(g)}\]

In this case, the \(N_2O\) molecules that react are express to those that take attached themselves to the surface of the solid goad. Once all of the sites on the limited surface of the catalyst take been occupied, additional gas-phase molecules must wait until the decomposition of ane of the adsorbed molecules frees up a surface site.

Enzyme-catalyzed reactions in organisms begin with the attachment of the substrate to the active site on the enzyme, leading to the germination of an enzyme-substrate complex. If the number of enzyme molecules is limited in relation to substrate molecules, then the reaction may appear to exist naught-lodge.

This is most often seen when two or more than reactants are involved. Thus if the reaction

\[ A + B \rightarrow \text{products} \tag{1}\]

is first-guild in both reactants and then that

\[\text{rate} = k [A][B] \tag{2}\]

If \(B\) is present in great backlog, so the reaction volition appear to be zero society in \(B\) (and first guild overall). This usually happens when \(B\) is as well the solvent that the reaction occurs in.

Differential Grade of the Zeroth Order Rate Law

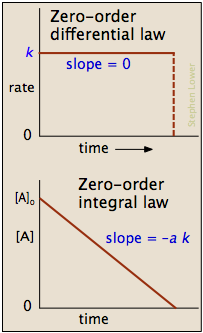
\[Rate = - \dfrac{d[A]}{dt} = k[A]^0 = k = constant \tag{3}\]

where \(Rate\) is the reaction rate and \(k\) is the reaction rate coefficient. In this example, the units of \(thousand\) are M/s. The units can vary with other types of reactions. For nothing-order reactions, the units of the rate constants are ever Yard/south. In higher order reactions, \(k\) will take dissimilar units.

Figure ane: Rate vs. time (A) and Concentration vs. fourth dimension for a nix order reaction.

Integrated Class of the Zeroth Lodge Rate Law

Integration of the differential rate police yields the concentration as a function of time. Outset with the full general rate police equations

\[Rate = k[A]^north \tag{4}\]

Starting time, write the differential form of the rate constabulary with \(north=0\)

\[Rate = - \dfrac{d[A]^0}{dt} = k \tag{5}\]

and so rearrange

\[{d}[A] = -kdt \tag{6}\]

Second, integrate both sides of the equation.

\[\int_{[A]_{0}}^{[A]} d[A] = - \int_{0}^{t} kdt \tag{seven}\]

Third, solve for \([A]\). This provides the integrated form of the rate police.

\[[A] = [A]_0 -kt \tag{8}\]

The integrated form of the rate law allows us to find the population of reactant at whatever time after the showtime of the reaction.

Graphing Aught-lodge Reactions

\[[A] = -kt + [A]_0 \tag{ix}\]

is in the form y = mx+b where slope = 1000 = -thou and the y- intercept = b = \([A]_0\)

Zero-order reactions are simply applicative for a very narrow region of fourth dimension. Therefore, the linear graph shown beneath (Figure 2) is only realistic over a limited time range. If we were to extrapolate the line of this graph downwards to represent all values of time for a given reaction, information technology would tell the states that as time progresses, the concentration of our reactant becomes negative. We know that concentrations can never exist negative, which is why zip-order reaction kinetics is applicative for describing a reaction for just brief window and must somewhen transition into kinetics of a dissimilar order.

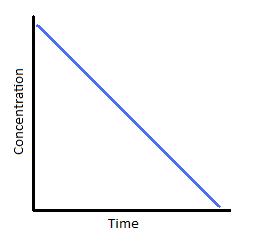
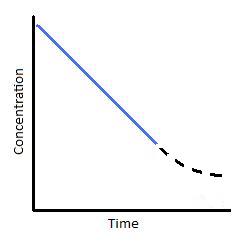
Figure 2: (left) Concentration vs. time of a zero-order reaction. (Right) Concentration vs. time of a zero-club catalyzed reaction.

To understand where the above graph comes from, let us consider a catalyzed reaction. At the beginning of the reaction, and for small values of time, the rate of the reaction is constant; this is indicated past the blue line in Figures 2; correct. This state of affairs typically happens when a catalyst is saturated with reactants. With respect to Michaelis-Menton kinetics, this point of catalyst saturation is related to the \(V_{max}\). As a reaction progresses through time, nonetheless, it is possible that less and less substrate will demark to the catalyst. As this occurs, the reaction slows and we see a tailing off of the graph (Effigy 2; right). This portion of the reaction is represented by the dashed black line. In looking at this item reaction, nosotros can run across that reactions are not zero-order nether all weather. They are only zero-order for a express amount of time.

If we plot rate as a part of time, we obtain the graph below (Figure 3). Again, this only describes a narrow region of time. The gradient of the graph is equal to thou, the charge per unit constant. Therefore, k is abiding with fourth dimension. In improver, we can see that the reaction rate is completely independent of how much reactant yous put in.

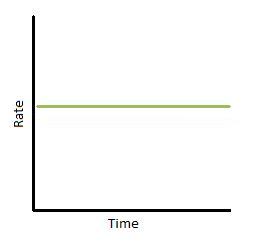
Figure 3: Rate vs. fourth dimension of a zero-club reaction.

Relationship Between One-half-life and Aught-lodge Reactions

The one-half-life. \(t_{i/2}\), is a timescale in which each one-half-life represents the reduction of the initial population to 50% of its original state. Nosotros tin correspond the human relationship by the following equation.

\[[A] = \dfrac{1}{two} [A]_o \tag{ten}\]

Using the integrated grade of the rate police force, we can develop a human relationship between naught-club reactions and the half-life.

\[[A] = [A]_o - kt \tag{11}\]

Substitute

\[\dfrac{1}{2}[A]_o = [A]_o - kt_{\dfrac{1}{2}} \tag{12}\]

Solve for \(t_{i/2}\)

\[t_{i/two} = \dfrac{[A]_o}{2k} \tag{xiii}\]

Notice that, for nil-order reactions, the half-life depends on the initial concentration of reactant and the rate constant.

Questions

1. Using the integrated grade of the charge per unit police force, determine the rate constant k of a zippo-order reaction if the initial concentration of substance A is 1.5 M and later 120 seconds the concentration of substance A is 0.75 1000.
2. Using the substance from the previous trouble, what is the half-life of substance A if its original concentration is i.ii G?
3. If the original concentration is reduced to one.0 M in the previous problem, does the half-life subtract, increase, or stay the aforementioned? If the half-life changes what is the new half-life?
4. Given are the charge per unit constants k of three different reactions:

• Reaction A: k = 2.3 Chiliad^-1due south^-1
• Reaction B: k = one.8 Ms^-ane
• Reaction C: k = 0.75 southward^-i

Which reaction represents a zero-society reaction?

5. True/False: If the rate of a aught-order reaction is plotted as a role of fourth dimension, the graph is a strait line where \( rate = k\ ).

Answers

1. The rate constant k is 0.00624 M/due south
2. The one-half-life is 96 seconds.
3. Since this is a zero-social club reaction, the half-life is dependent on the concentration. In this instance, the one-half-life is decreased when the original concentration is reduced to 1.0 K. The new half-life is 80 seconds.
4. Reaction B represents a null-guild reaction because the units are in M/s. Zero-order reactions always take rate constants that are represented past molars per unit of fourth dimension. Higher order reactions, all the same, require the charge per unit constant to be represented in dissimilar units.
5. True. When using the rate function \( rate = 1000[A]^due north \) with n equal to zero in zero-club reactions. Therefore, rate is equal to the rate abiding 1000.

Summary

The kinetics of whatsoever reaction depend on the reaction mechanism, or rate law, and the initial conditions. If nosotros assume for the reaction A -> Products that there is an initial concentration of reactant of [A]₀ at time t=0, and the rate police force is an integral order in A, so we tin summarize the kinetics of the naught-club reaction as follows:

References

• Petrucci, Ralph H., William Due south. Harwood, Geoffrey Herring, and Jeffry D. Madura. Full general Chemistry: Principles & Modern Applications. Ninth ed. Upper Saddle River, N.J.: Pearson Education, 2007. Print.

Contributors and Attributions

• Rachael Curtis, Jessica Martin, David Cao

smithlosead.blogspot.com

Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Kinetics/02:_Reaction_Rates/2.10:_Zero-Order_Reactions

Share this post